√Teorema Phytagoras ~ Keminjal
Diantara sekian banyak situs di internet yang membahas mengenai Teorema Phytagoras, tapi mengapa Anda memilih untuk mengunjungi situs ini? Tentunya hal tersebut bukan tanpa alasan bukan? Dan yang tahu jawaban dari pertanyaan diatas adalah Anda sendiri bukan? hehehe, Oke tanpa berpanjang kata, yuk langsung disimak saja ulasan lengkap Teorema Phytagoras dibawah ini.
Ulasan Lengkap Teorema Phytagoras
Teorema Phytagoras merupakan seuah aturan matematika yang bisa dipakai dalam menentukan panjang salah satu sisi dari suatu segitiga siku-siku.
Yang perlu kalian ingat dari teorema ini yaitu teorema hanya berlaku untuk segitiga siku-siku. Maka dari itu tidak dapat digunakan untuk menentukan sisi dari sebuah segitiga lain yang tidak berbentuk siku-siku.
Teorema pythagoras masuk ke dalam salah satu materi dalam mata pelajaran matematika dasar yang mempunyai perluasan serta manfaat yang sangat banyak.
Materi ini juga sangat banyak dimanfaatkan serta sangat sering keluar dalam soal-soal ujian nasional.
Pada dasarnya, teorema pythagoras sangatlah sederhana yakni kita hanya diminta untuk menghitung panjang sisi dari suatu segitiga siku-siku di mana sisi lainnya telah kita ketahui.
Jikalau sisi lain belum diketahui paling tidak dapat kita cari dengan menggunakan cara lain sebelumnya.
Pembahsan selengkapnya mengenai teorema pythagoras silahkan simak baik-baik ulasan berikut ini.
Sifat Teorema Pythagoras
Terdapat dua sifat yang ada dalam teorema pythagoras, diantaranya yaitu:
- Hanya untuk segitiga siku-siku
- Minimal 2 sisinya dapat diketahui terlebih dahulu
Permasalahan lain yang sering dijumpai yaitu dalam mengidentifikasi suatu segitiga siku-siku.
Bagian mana sisi miringnya, serta sisi lainnya. Untuk itu akan kami berikan sebuah segitiga siku-siku serta mengajak kalian untuk memahami setiap komponen dari segi tiga siku-siku.
Namun sebelum itu, yuk ketahui telebih dahulu karakteristik dari suatu segitiga, berikut ulasan selengkapnya.
Karakteristik Suatu Segitiga
- Apabila kuadrat sisi miring = jumlah kuadrat sisi yang lain, maka segitiga tersebut merupakan segitiga siku-siku.
- Apabila kuadrat sisi miring < jumlah kuadrat sisi yang lain, maka segitiga tersebut merupakan segitiga lancip.
- Apabila kuadrat sisi miring > jumlah kuadrat sisi yang lain, maka segitiga tersebut merupakan segitiga tumpul.
Mengidentifikasi Sebuah Segitiga Siku-siku
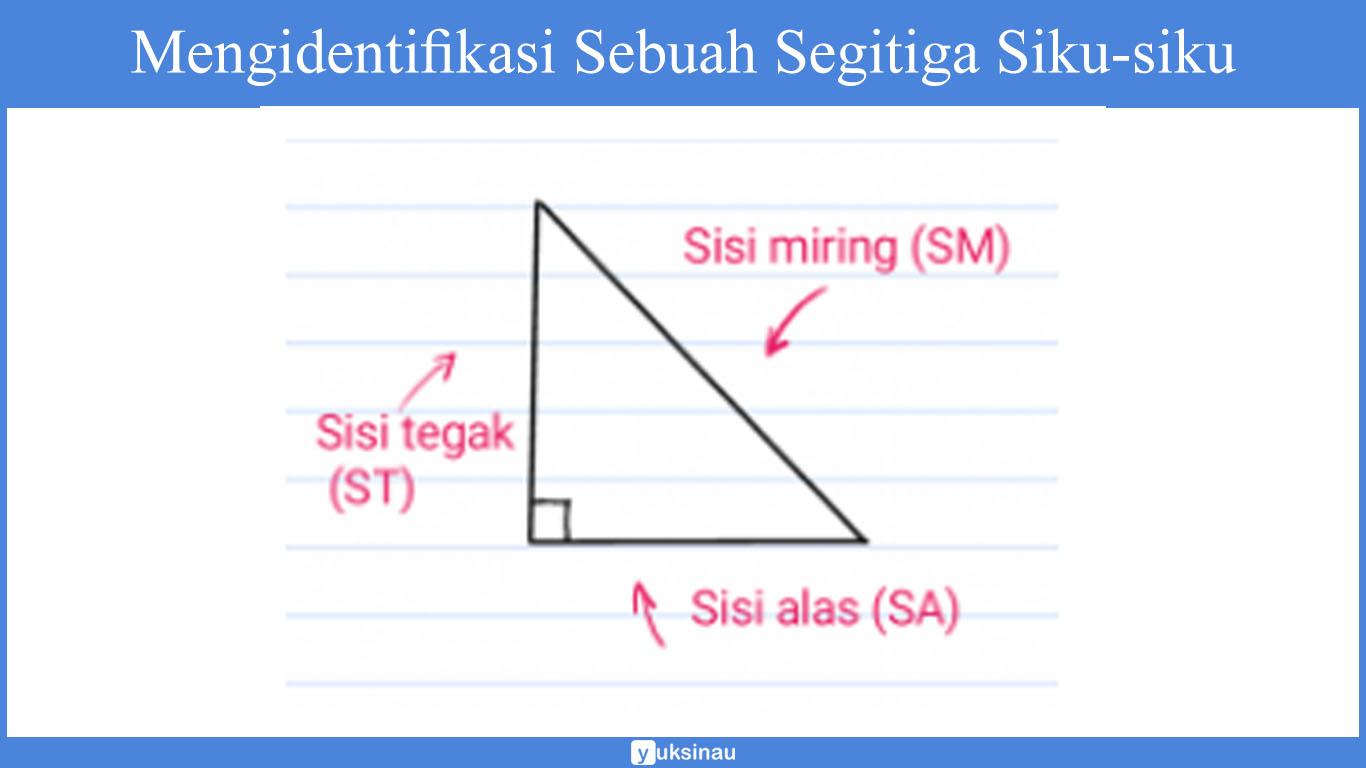
memberi nama sisi segitiga untuk diingat
Apabila kalian perhatikan gambar di atas, maka dapat kalian jumpai tiga buah sisi yang telah kami beri nama pada setiap sisinya.
Sisi miring yang disingkat sebagai (SM), sisi alas yang disingkat sebagai (SA), serta sisi tegak yang disingkat sebagai (ST).
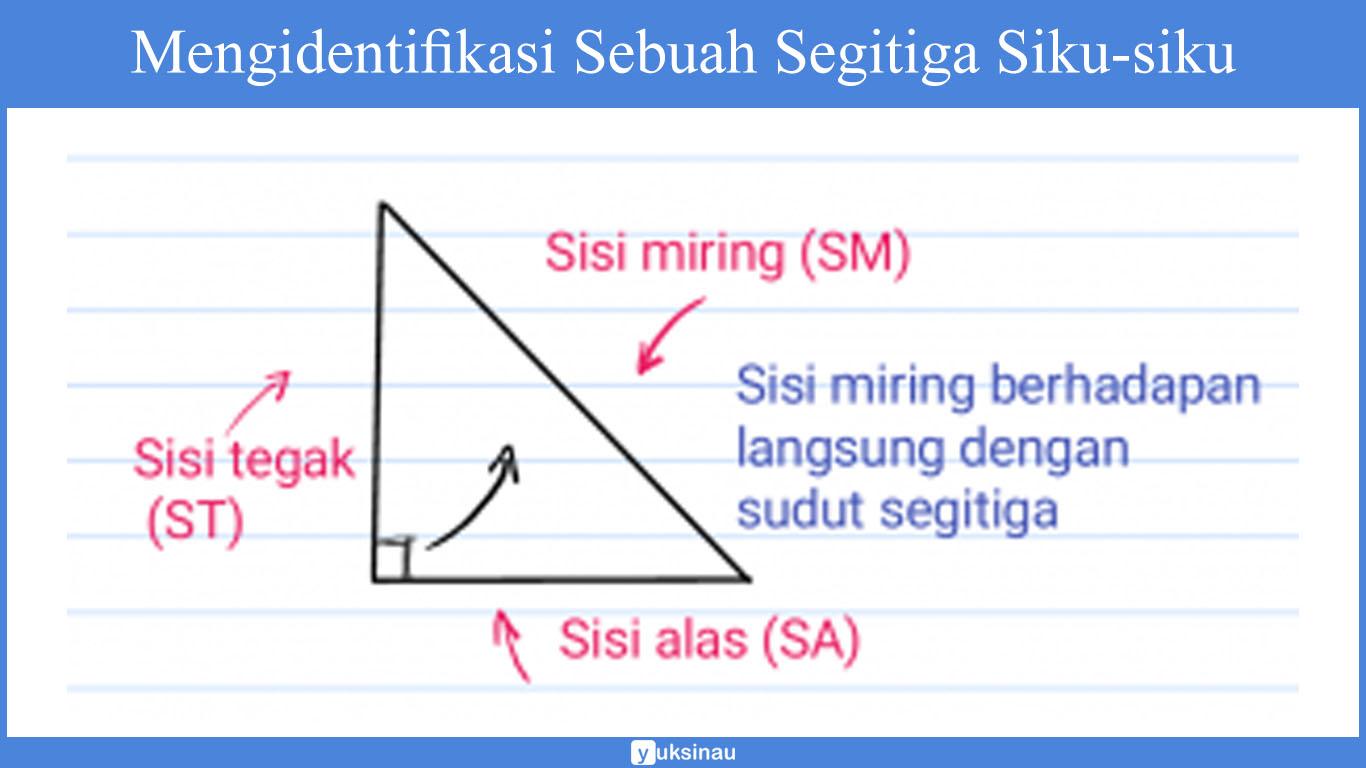
Dalam gambar di atas bisa kita jumpai jika sisi miring berada tepat di depan siku-siku dari sebuah segitiga tersebut.
Siku-siku pada umumnya digambarkan dengan sebuah kotak kecil di dalamnya, seperti gambar di atas yang ditunjuk dengan panah hitam.
Sisi miring tersebut berhadapan langsung dengan sudut siku-siku dari segi tiga di atas. Untuk sisi alas dan juga sisi tegaknya sebenarnya tidak terlalu bermasalah jika kalian keliru dalam mengidentifikasi nya.
Mengapa kalian butuh untuk memperhatikan dan memahami bentuk sebuah segitiga siku-siku?
Karena, agar jika kalian menjumpai segitiga siku-siku nya di balik atau diganti namanya kalian tidak akan mengalami kesuliatan.
Itulah mengapa kalian butuh untuk memahami sekaligus mengidentifikasi suatu segitiga siku-siku.
Sebagai contoh, perhatikan baik-baik gambar di bawah ini:

Walaupun segitiga siku-siku tersebut sudah kita balik, kalian telah mampu mengidentifikasi sisi miring, sisi alas, dan sisi tegaknya.
Pada gambar di atas sisi miring yaitu sisi r, sisi alasnya yaitu sisi p, serta sisi tegaknya yaitu sisi q.
Selanjutnya yang juga menjadi permasalahan yang paling banyak menyesatkan yaitu kesalahan dalam menghafal rumus teorema pythagoras.
Berikut ulasan selengkapnya.
Rumus Teorema Pythagoras
Rumus Phytagoras merupakan rumus yang diperoleh dari materi Teorema Phytagoras.
Teorema Phytagoras sendiri seperti yang telah dissebutkan di atas merupakan teorema yang menerangkan tentang hubungan antara sisi-sisi yang ada dalam sebuah segitiga siku-siku.
Teorema ini pertama kali dikemukakan oleh seorang matematikiawan yang berasal dari Yunani bernama Phytagoras.
Adapun bunyi atau dalil Teorema Phytagoras yaitu sebagai berikut:
Pada suatu segitiga siku-siku, kuadrat dari sisi terpanjang yaitu sama dengan hasil jumlah dari kuadrat sisi-sisi penyikunya.
Dari teorema tersebut bisa kita bikin suatu rumus yang bisa kita gambarkan seperti di bawah ini:
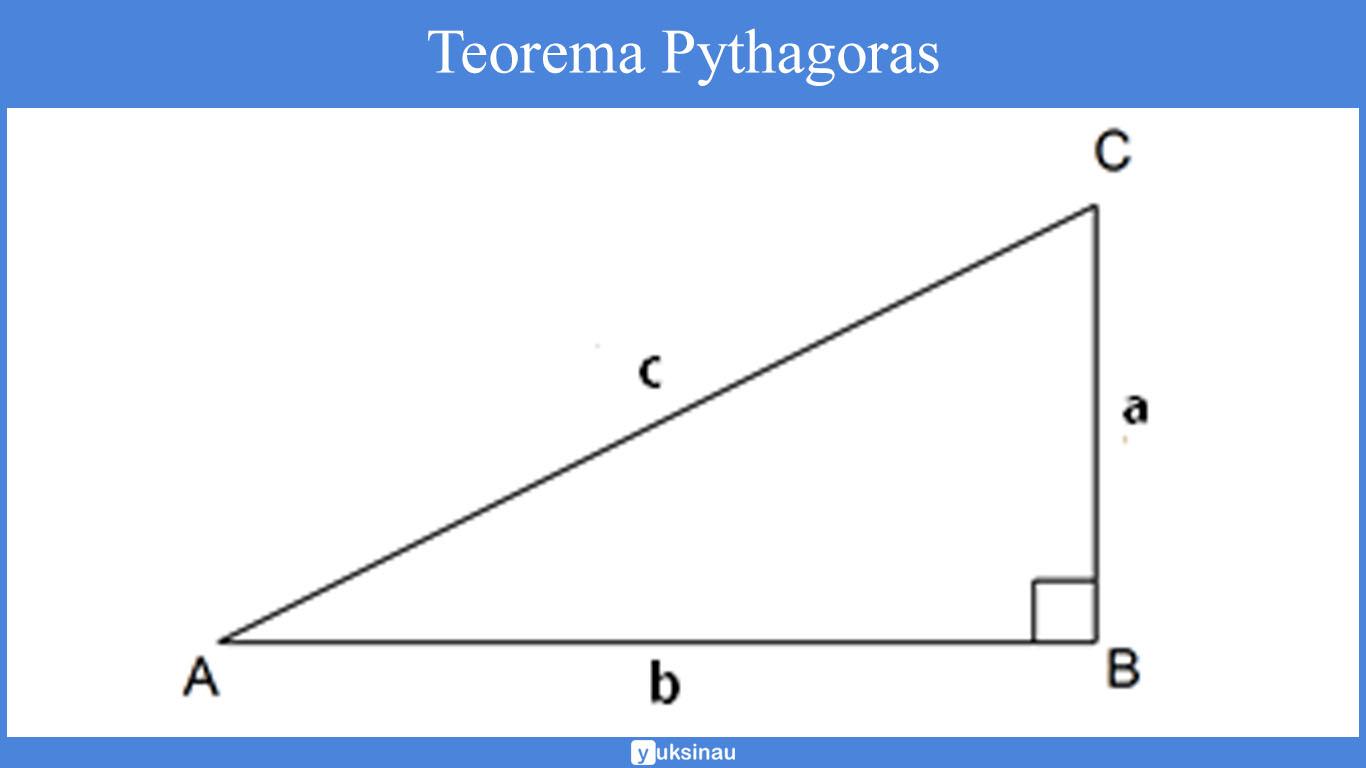
Sebagai contoh, diketahui sebuah segitiga dengan siku-siku di B. Apabila panjang sisi miring (hipotenusa) yaitu c serta panjang sisi-sisi penyikunya (sisi selain sisi miring) yaitu a dan b. Maka teorema Phytagoras di atas bisa kita rumuskan seperti berikut ini:
Rumus Phytagoras
c² = a² + b²
Keterangan:
c = sisi miring
a = tinggi
b = alas
Rumus Phytagoras pada umumnya dipakai dalam mencari panjang sisi miring segitiga siku-siku seperti berikut ini:

Kuadrat sisi AC = kuadrat sisi AB + kuadrat sisi BC. atau AC² = AB² + BC²
Rumus untuk mencari panjang sisi alas yaitu:
b² = c² – a²
Rumus untuk mencari sisi samping atau tinggi segitiga yaitu:
a² = c² – b²
Rumus untuk mencari sisi miring segitiga siku-siku yaitu:
c² = a² + b²
Kegunaan Dalil Teorema Phytagoras
Selain dimanfaatkan dalam menentukan panjang salah satu sisi segitiga yang tidak diketahui, dalil atau bungi dari Pythagoras ini juga bisa dipakai dalam beberapa perhitungan, diantaranya yaitu:
- Menentukan panjang diagonal persegi
- Menentukan diagonal ruang kubus dan juga balok
Berikut akan kami berikan penjelasan dari masing-masing kegunaanya:
1. Menentukan panjang diagonal persegi
Diberikan suatu persegi panjang ABCD seperti yang terlihat pada gambar di bawah ini:
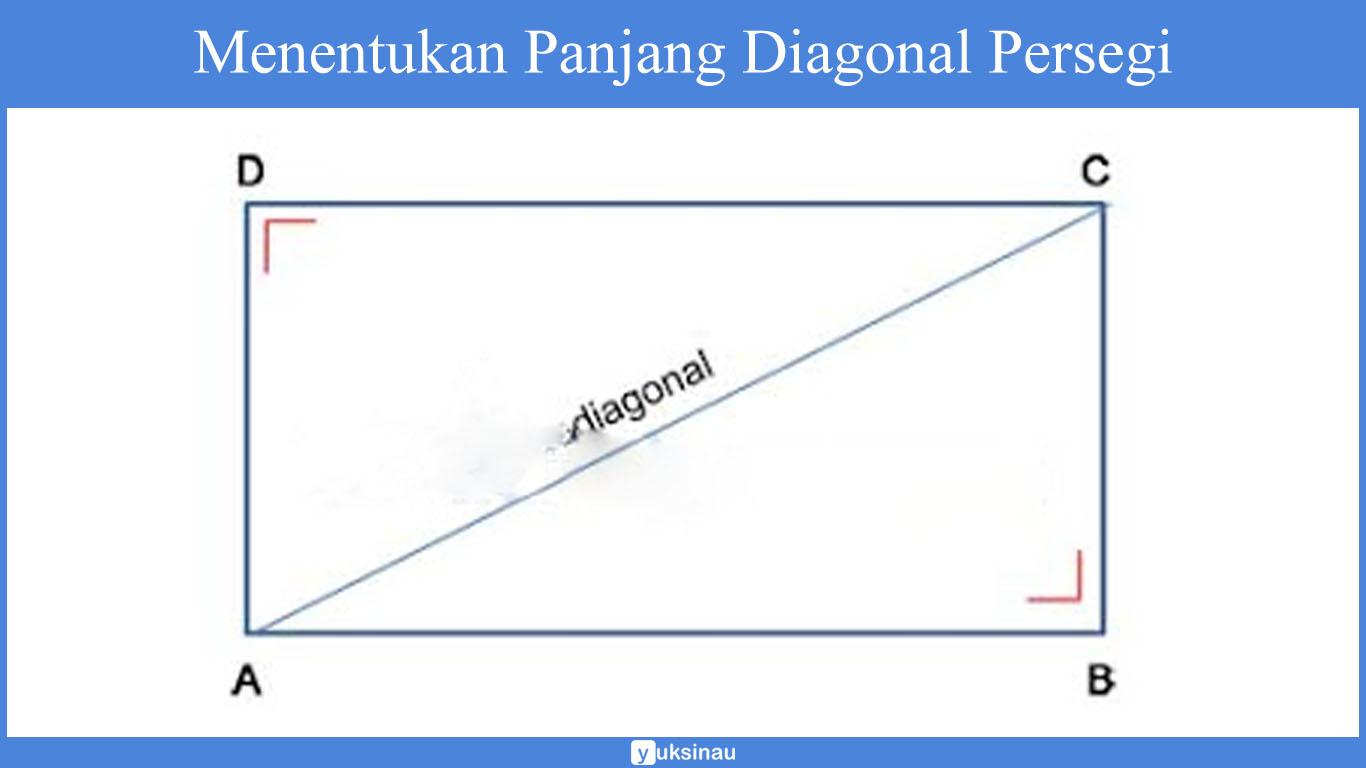
Garis AC merupakan garis diagonal persegi. Apabila panjang sisi-sisi persegi tersebut diketahui, maka panjang diagonalnya bisa kita hitung dengan menggunakan dalil Pythagoras seperti berikut:
AC2 = AB2 + BC2
AC2 = AD2 + CD2
Contoh soal:
Sebuah persegi ABCD mempunyai panjang 8 cm dan lebar 6 cm. Tentukanlah panjang diagonal dari persegi tersebut.
Jawab:
Diketahui:
- panjang = p = 8 cm
- lebar = L = 6 cm
Ditanya:
- diagonal = d = … ?
Berdasarkan dalil Pythagoras, maka:
⇒ d2 = p2 + L2
⇒ d2 = 82 + 62
⇒ d2 = 64 + 36
⇒ d2 = 100
⇒ d = √100
⇒ d = 10 cm
Sehingga, panjang diagonal persegi pada soal di atas adalah 10 cm.
2. Menentukan diagonal ruang kubus dan juga balok
Diberikan suatu balok ABCD.EFGH seperti yang terlihat pada gambar di bawah ini:
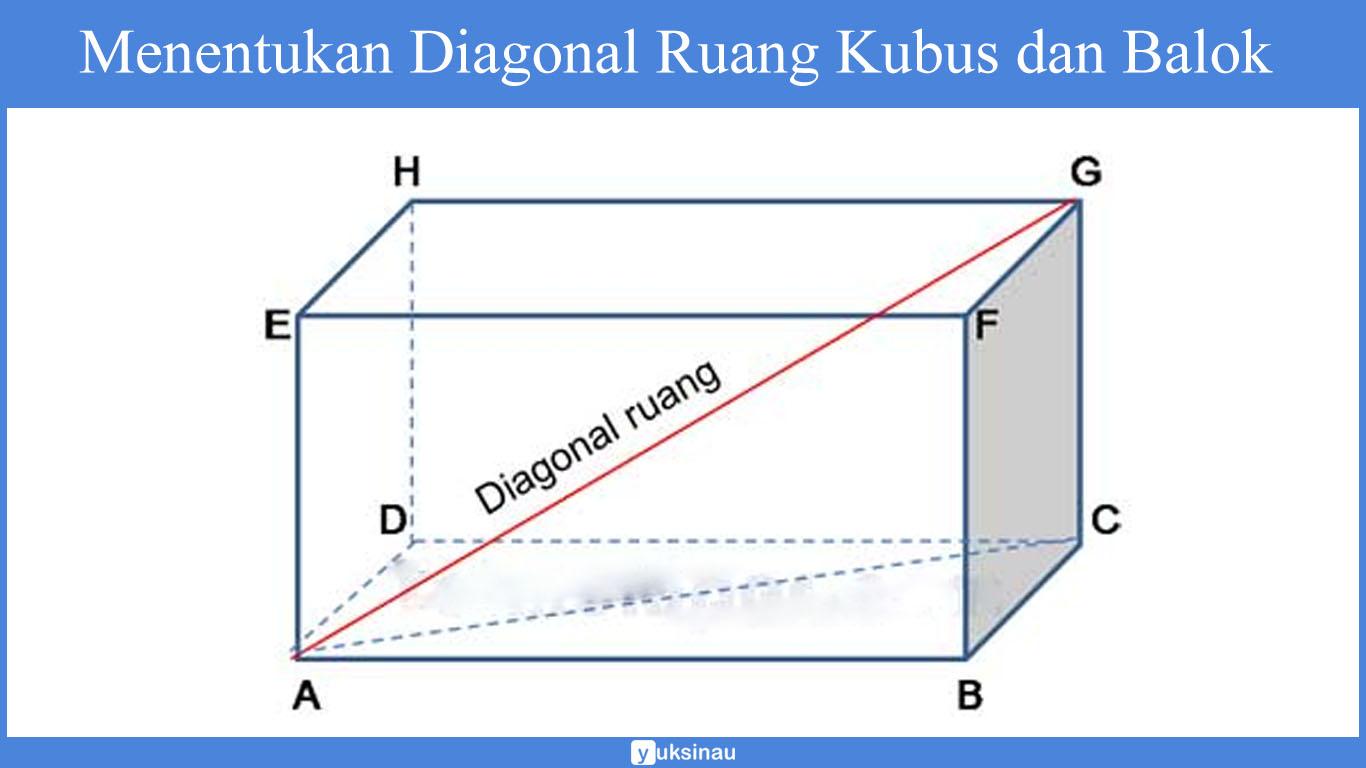
Garis AG merupakan salah satu diagonal ruang dalam balok tersebut. Panjang diagonal ruang AG bbisa kita hitung erdasarkan dalil Pythagoras seperti berikut ini:
AG2 = AC2 + CG2
Keterangan:
AG = diagonal ruang
CG = tinggi balok
AC = diagonal bidang alas
Kemudian perhatikan alas balok yakni persegi ABCD. Berdasarkan dari bunyi Pythagoras, panjang diagonal bidang AC bisa kita hitung dengan menggunakan rumus berikut:
AC2 = AB2 + BC2
Keterangan:
AB = panjang balok
BC = lebar balok
Sebab, AC2 = AB2 + BC2, maka rumus panjang diagonal ruang AG bisa kita ubah menjadi:
⇒ AG2 = AC2 + CG2
⇒ AG2 = AB2 + BC2 + CG2
⇒ AG2 = p2 + L2 + t2
Sehingga, rumusnya akan menjadi:
dr2 = p2 + L2 + t2
Keterangan:
dr = diagonal ruang
p = panjang balok
L = lebar balok
t = tinggi balok
Contoh soal:
Suatu balok memiliki panjang, lebar, dan tinggi berturut-turut yaitu 12 cm, 9 cm, dan 8 cm. Tentukanlah panjang salah satu diagonal ruangnya!
Jawab:
Diketahui:
- p = 12 cm
- L = 9 cm
- t = 8cm
Ditanya:
- dr = … ?
Berdasarkan dari bunyi atau dalil Pythagoras, maka:
⇒ dr2 = p2 + L2 + t2
⇒ dr2 = 122 + 9sup>2 + 82
⇒ dr2 = 144 + 81 + 64
⇒ dr2 = 289
⇒ dr = √289
⇒ dr = 17 cm
Sehingga, panjang diagonal ruangnya yaitu 17 cm.
Menentukan Panjang Sisi Segitiga Siku-Siku
Secara matematis, rumus dari Phytagoras biasa dipakai untuk menentukan panjang sisi dari suatu segitiga siku-siku.
Untuk lebih jelasnya, perhatikan beberapa contoh soal di bawah ini.
Contoh Soal Pythagoras (Pitagoras) dan Penyelesaiannya
Soal 1.
Diketahui segitiga siku-siku ABC dengan siku-siku di B yang digambarkan sebagai berikut:
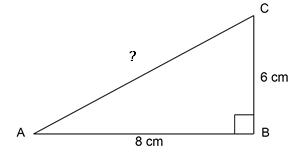
Tentukan panjang sisi miring AC pada gambar di atas!
Jawab:
Sebab segitiga di atas adalah segitiga siku-siku, maka berlaku rumus Phytagoras seperti betikut ini:
AC² = AB² + BC²
AC² = 8² + 6²
AC² = 64 + 36
AC² = 100
AC = √100
AC = 10
Sehingga, panjang sisi AC dalam segitiga siku-siku tersebut yaitu 10 cm.
Soal 2.
Suatu segitiga siku-siku KLM dengan siku-siku di L digambarkan seperti di bawah ini:

Tentukan panjang sisi KL pada gambar di atas!
Jawab:
Sebab, segitiga di atas adalah segitiga siku-siku, maka berlaku rumus Phytagoras seperti berikut ini:
KM² = KL² + LM²
KL² = KM² – LM²
KL² = 13² – 12²
KL² = 169 – 144
KL² = 25
KL = √25
KL = 5
Sehingga, panjang sisi KL dalam segitiga siku-siku di atas yaitu 5 cm.
Soal 3.
Diketahui segitiga siku-siku DEF dengan siku-siku di E digambarkan seperti di bawah ini:
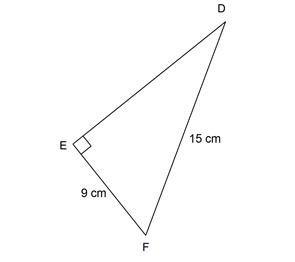
Tentukan panjang sisi DE pada gambar di atas!
Jawab:
Sebab segitiga DEF di atas merupakan segitiga siku-siku, maka berlaku rumus Phytagoras seperti di bawah ini:
DF² = DE² + EF²
DE² = DF² – EF²
DE² = 15² – 9²
DE² = 225 – 81
DE² = 144
DE = √144
DE = 12
Sehingga, panjang sisi DE pada segitiga siku-siku di atas yaitu 12 cm.
Soal 4.
Diketahui segitiga siku-siku ABC dengan siku-siku berada di B. Apabila panjang sisi AB = 16 cm serta Panjang sisi BC = 12 cm.
Maka hitunglah panjang sisi AC pada segitoga di atas!
Jawab:
Dari soal di atas bisa kiat gambarkan sebuah segitiga siku-siku seperti berikut ini:

Sebab segitiga di atas adalah segitiga siku-siku, maka berlaku rumus Phytagoras seperti di bawah ini:
c² = a² + b²
c² = 12² + 16²
c² = 144 + 256
c² = 400
c = √400
c = 20
Sehingga, panjang sisi AC pada segitiga siku-siku ABC dalam soal di atas yaitu 20 cm.
Menentukan Jenis Segitiga jika Diketahui Panjang Sisinya
Selain untuk mencari panjang sisi segitiga siku-siku, rumus Phytagoras juga dipakai dalam menentukan jenis dari suatu segitiga.
Apakah suatu segitiga termasuk dalam jenis segitiga siku-siku, segitiga lancip, ataupun segitiga tumpul. Kemudian, bagaimana caranya untuk menentukan jenis segitiga dengan rumus Phytagoras itu?
Untuk menentukan jenis segitiga dengan menggunakan teorema Phytagoras, maka kita harus membandingkan kuadrat dari sisi terpanjang dengan hasil jumlah dari kuadrat sisi-sisi penyikunya.
Sebaai contoh, diketahui sebuah segitiga siku-siku dengan panjang sisi miringnya (sisi terpanjang) yaitu c. Serta panjang sisi-siki penyikunya yaitu a dan b, sehingga:
- Apabila c² < a² + b², maka segitiga tersebut termasuk segitiga lancip;
- Apabila c² = a² + b², maka segitiga tersebut termasuk segitiga siku-siku;
- Apabila c² > a² + b², maka segitiga tersebut termasuk segitiga tumpul.
Untuk lebih jelasnya, perhatikan beberapa contoh soal di bawah ini:
Soal 1.
Suatu segitiga siku-siku ABC dengan siku-siku berada di B. Tentukan jenis segitiga tersebut jika telah diketahui panjang sisi AB = 8 cm, BC = 15 cm, dan AC = 20 cm!
Jawab:
Misalnya a merupakan sisi terpanjang dan b, c merupakan dua sisi lainnya, maka dapat kita ketahui jika:
- c = 20 cm
- b = 8 cm
- a = 15 cm.
c² = 20² = 400
a² + b² = 8² + 15² = 64 + 225 = 289
Sebab,
c² > a² + b²
400 > 289
Sehingga, segitiga ABC termasuk ke dalam segitiga tumpul.
Soal 2.
Tentukan jenis segitiga berikut apabila diketahui panjang sisi-sisinya yaitu 10 cm, 12 cm, dan 15 cm!
Jawab:
Misalknya c merupakan sisi terpanjang dan b, a merupakan dua sisi lainnya, maka dapat kita ketahui:
- c = 15 cm
- b = 10 cm
- a = 12 cm.
c² = 15² = 225
a² + b² = 12² + 10² = 144 + 100 = 344
Sebab,
c² < a² + b²
225 < 344
Sehingga, segitiga tersebut termasuk ke dalam segitiga lancip.
Tripel Phytagoras
Perhatikan beberapa contoh bilangan yang ada di bawah ini:
3, 4, dan 5
6, 8, dan 10
5, 12, dan 13
Beberapa bilangan yang disebutkan di atas meripakan bilangan-bilangan yang memenuhi aturan rumus Phytagoras.
Di mana bilangan tersebut disebut sebagai Tripel Phytagoras. Adapun bilangan Tripel Phytagoras bisa didefinisikan sebagai berikut.
Tripel Phytagoras merupakan berbagai bilangan bulat positif yang kuadrat bilangan terbesarnya mempunyai nilai yang sama dengan jumlah dari kuadrat bilangan-bilangan lainnya.
Pada umumnya, Tripel Phytagoras terbagi menjadi dua macam, yakni Tripel Phytagoras Primitif dan Tripel Phytagoras Non-Primitif.
Tripel Phytagoras Primitif merupakan Tripel Phytagoras yang di mana seluruh bilangannya mempunyai FPB sama dengan 1.
Seabgai contoh, dari bilangan Tripel Phytagoras Primitif yaitu antara lain: 3, 4, dan 5 serta 5, 12, 13.
Sementara untuk Tripel Phytagoras Non-Primitif merupakan Tripel Phytagoras di mana bilangannya mempunyai FPB yang tidak hanya sama dengan satu.
Sebagai contoh yaitu:6, 8, dan 10; 9, 12, dan 15; 12, 16, dan 20; dan juga 15, 20, dan 25.
Pola angka pythagoras (Triple pythagoras) berfungi guna menyelesaikan soal pythagoras dengan mudah, berikut pola angka (triple pythagoras) tersebut yaitu:
a – b – c
3 – 4 – 5
5 – 12 – 13
6 – 8 – 10
7 – 24 – 25
8 – 15 – 17
9 – 12 – 15
10 – 24 – 26
12 – 16 – 20
12 – 35 – 37
13 – 84 – 85
14 – 48 – 50
15 – 20 – 25
15 – 36 – 39
16 – 30 – 34
17 – 144 – 145
19 – 180 – 181
20 – 21 – 29
20 – 99 – 101
Dan masih banyak yang lainnya.
Keterangan:
a = tinggi segitiga
b = alas segitiga
c = sisi miring
Cara menentukan bilangan tripel pythagoras:
Apabila a dan b bilangan bulat positif dan a > b, maka tripel pythagoras bisa kita cari dengan menggunakan rumus seperti berikut ini:
2ab,a2 – b2, a2 + b2
Untuk lebih jelasnya perhatikan tabel di bawah ini:

Aplikasi Rumus Phytagoras dalam Permasalahan Sehari-Hari
Rumus Phytagoras banyak kita jumpai dalam berbagai kegiatan sehari-hari. Berikut ini akan kami berikan ulasan mengenai beberapa aplikasi rumus Phytagoras tersebut.
Contoh Soal Menentukan Jarak Kaki Tangga dengan Tembok
Perhatikan baik-baik gambar di bawah ini:
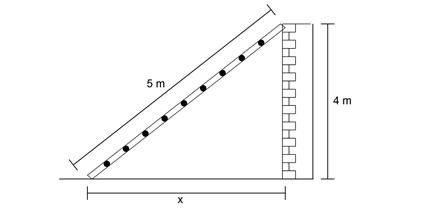
Diketahui suatu tangga disandarkan pada tembok. Apabila panjang tangga yaitu 5 m serta tinggi temboknya yaitu 4 m. Maka hitunglah jarak antara kaki tangga dengan temboknya!
Jawab:
Misalnya jarak antara kaki tangga dengan tembok yaitu x, maka untuk menentukan nilai x bisa kita pakai Rumus Phytagoras seperti berikut ini:
Diketahui:
- sisi miring atau c = 5m
- tinggi atau b = 4m
Ditanyakan:
- alas atau x?
x² = c² – b²
c² = 5² – 4²
c² = 25 – 16
c² = 9
c = √9
c = 3
Sehingga, jarak antara kaki tangga dengan tembok yaitu 3 m.
Contoh Soal Menentukan Jarak Titik Awal Keberangkatan ke Titik Akhir
Perhatikan baik-baik gambar di bawah ini:

Suatu kapal berlayar dari pelabuhan A ke pelabuhan B sejauh 15 km menuju arah utara. Seudah tiba pada Pelabuhan B, kapal tersebut berlayar kembali sejauh 36 km menuju arah timur. Tentukan jarak antara pelabuhan A dengan titik akhir!
Jawab:
Dari soal di atas bisa kita bikin suatu gambar dengan informasi seperti yang terdapat pada penyelesaian di bawah ini:
Ditanyakan:
- sisi miring atau c
Diketahui:
- b = 36km
- a = 15km
Sehingga:
Jarak pelabuhan A ke titik akhir yaitu:
c² = 15² + 36²
c² = 225 + 1296
c² = 1521
c = √1521
c = 39
Maka, jarak pelabuhan A ke titik akhir yaitu sejauh 39 km.
Demikianlah ulasan singkat kali ini mengenai Teorema Phytagoras yang dapat kami sampaikan. Semoga ulasan di atas mengenai mengenai Teorema Phytagoras dapat kalian jadikan sebagai bahan belajar kalian.
The post Teorema Phytagoras appeared first on Yuksinau.
Itulah tadi ulasan tentang Teorema Phytagoras yang dapat kami sampaikan untuk Sobat pembaca semuanya. Tak lupa kami ucapkan banyak terima kasih karena sudah mengunjungi situs keminjal. blogspot. com dan membaca urian diatas hingga selesai. Semoga apa yang kami sampaikan diatas dapat menambah wawasan kita semuanya, tertama untuk Anda yang memang sedang mencarinya. Ingat untuk selalu bahagia dan sampai jumpa di postingan selanjutnya.
Post a Comment for "√Teorema Phytagoras ~ Keminjal"