√Sin Cos Tan ~ Keminjal
Diantara sekian banyak situs di internet yang membahas mengenai Sin Cos Tan, tapi mengapa Anda memilih untuk mengunjungi situs ini? Tentunya hal tersebut bukan tanpa alasan bukan? Dan yang tahu jawaban dari pertanyaan diatas adalah Anda sendiri bukan? hehehe, Oke tanpa berpanjang kata, yuk langsung disimak saja ulasan lengkap Sin Cos Tan dibawah ini.
Ulasan Lengkap Sin Cos Tan
Jika kalian belajar matematika, pasti sempat mendengar yang namanya trigonometri, dimana di dalam trigonometri tersebut terdapat istilah sin cos tan.
Trigonometri sendiri merupakan suatu cabang ilmu matematika yang mempelajari hubungan antara besar sudut dengan panjang sisi segitiga.
Jika diartikan secara harfiah, trigonometri asalnya dari bahasa Yunani, yakni trigonon yang mempunyai arti “tiga sudut” serta metron yang berarti “mengukur”.
Nah berikut ini akan kita bahas secara tuntas terkait trigonometri sin cos tan, simak baik – baik ulasan berikut ya.
Pengertian Sin Cos Tan
Sebelum kalian melihat tabel nilai dari cos sin tan trigonometri, sebaiknya kalian mengetahui pengertian dari sin cos tan trigonometri itu sendiri, diantaranya yaitu:
- Sin (sinus) merupakan suatu perbandingan panjang pada suatu segitiga yaitu antara sisi depan sudut dengan sisi miring segitiga, y/z.
- Cos (cosinus) merupakan suatu perbandingan panjang pada suatu segitiga yaitu diantara sisi samping sudut dengan sisi miringnya, x/z.
- Tan (tangen) merupakan suatu perbandingan panjang pada suatu segitiga diantara sisi depan sudut serta sisi samping segitiga, y/x.
Untuk lebih jelasnya mengenai uraian di atas, perhatikan gambar yang ada dibawah ini:

Catatan:
Semua perbandingan trigonometri sin cos tan di atas terbatas yaitu hanya berlaku untuk objek segitiga siku siku / segitiga yang mana salah satu sudutnya memiliki nilai 90 derajat.
Trigonometri banyak dimanfaatkan di dalam Bidang Sains dan teknik. Trigonometri digunakan dalam bidang pemetaan, pengukuran, statistik, listrik, optik, dan lainnya.
Sudut Sin Cos Tan
Di dalam sin cos tan trigonometri terdapat istilah sudut sudut istimewa, berikut tabelnya:
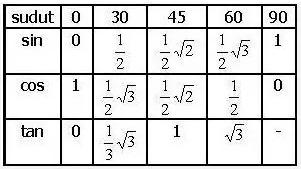
Nah,untuk memahami serta menghafalkan sudut – sudut trigonometri, kalian harus hafal terlebih dahulu tabel sudut – sudut istimewa diatas.
Jika kalian sudah paham dan hafal, maka selanjutnya kalian pahami konsep kuadran I, II, III dan IV berikut ini:

Keterangan:
- Di kuadran I (0 – 90) , seluruh nilai sin, tan serta cos memiliki nilai positif → “semua”.
- Di kuadran II (90 – 180) , hanya sin yang nilainya positif → sin dibaca “sindikat”
- Di kuadran II (180 – 270) , hanya tan yang nilainya positif → tan dibaca “tangan / tangen”
- Di kuadran II (270 – 360) , hanya cos yang nilainya positif → cos dibaca “kosong”.
Sehingga untuk memudahkan kalian dalam mengingat gambar di atas, kalian hanya perlu menghafalkan kalimat: “Semua Sindikat Tangannya Kosong“.
Perubahan Sudut

Apabila kalian nanti diminta untuk menghafalkan seluruh sudut pada trigonometri, maka pastinya kalian akan mengalami kesulitan apabila tidak mengetahui konsepnya.
Contohnya jika diberi pertanyaan : Berapa sin 330 ? Cos 315? tan 300 dan lainnya.
Pertanyaan terkait sudut trigonometri yang tidak terdapat di dalam tabel sudut istimewa tentunya akan sangat membingungkan apabila kalian tidak tau cara praktisnya.
Berikut informasi selengkapnya:
Contoh Soal Menghitung Sudut Trigonometri:
Contoh 1
Hitunglah nilai dari cos 210!
Jawab:
Diketahui:
- cos 210 → berada pada kuadran III → pasti negatif, sehingga jawabannya juga harus negatif.
Penyelesaian:
cos 210 = cos (180 +30) = – cos 30 = -1/2√3
Sehingga dapat diketahui nilai cos 210 = – 1/2 √3 (minus setengah akar tiga).
Contoh 2
Hitunglah nilai sin 300 ?
Jawab:
Diketahui:
- sin 300 → berada pada kuadran IV → pasti negatif, sehingga jawabannya juga harus negatif.
Penyelesaian:
sin 300 = sin (270 + 30) = – cos 30 = 1/2√3
Sehingga dapat diketahui nilai sin 300 = – 1/2 √3 (minus setengah akar tiga).
Apabila kalian masih juga bingung, berikut kita ringkas kembali.
Kita gunakan KONSEP: Misalkan diketahui sudut sebesar x.
Apabila kalian hendak merubah sudut x ke dalam sudut y, maka kalian bisa memakai patokan pada nilai 90, 180, 270, serta 360.
Contoh:
- Sudut 210 = sudut (180 + 30) atau sudut 210 = sudut (270 – 60).
Yang perlu kalian ingat, kalian harus merubah sudut di atas sehingga mengandung sudut – sudut istimewa di kuadran satu seperti 30, 45, 60, sehingga mudah untuk mencari nilainya.
Sehingga dapat kita simpulkan, pada perubahan sudut terdapat beberapa hal penting seperti:
Apabila kalian memakai 90 dan 270, maka konsepnya adalah “BERUBAH”:
- sin berubah menjadi cos
- cos berubah menjadi sin
- tan berubah menjadi cotan
Apabila kalian memakai 180 dan 360, maka konsepnya adalah “TETAP”:
- sin tetap menjadi sin
- cos tetap menjadi cos
- tan tetap menjadi tan
Berikut contoh soal kembali untuk pembahasan di atas:
Contoh 3
Hitunglah nilai sin 150!
Jawab:
Diketahui:
- sin 150 → berada pada kuadran II→ pasti positif, sehingga jawabannya juga harus positif.
Penyelesaian:
sin 150 = sin (90 + 60) = + cos 60 = +1/2 (positif setengah) → ingat sudut 90 Konsep “BERUBAH”
atau
sin 150 = sin (180 – 30) = + sin 30 = +1/2 (positif setengah) → ingat sudut 180 memakai konsep “TETAP”.
Tabel Trigonometri
Berikut akan kami sajikan beberapa tabel trigonometri yang dibagi ke dalam beberapa kelompok, antara lain:
1. Tabel Sin Cos Tan Kuadran 1 dari 0º – 90º
| Sudut | 0º | 30º | 45º | 60º | 90º |
|---|---|---|---|---|---|
| Sin | 0 | 1/2 | 1/2 √2 | 1/2 √3 | 1 |
| Cos | 1 | 1/2 √3 | 1/2 √2 | 1/2 | 0 |
| Tan | 0 | 1/2 √3 | 1 | √3 | ∞ |
2. Tabel Sin Cos Tan Kuadran 2 dari 90º – 180º
| Sudut | 90º | 120º | 135º | 150º | 180º |
|---|---|---|---|---|---|
| Sin | 1 | 1/2 √3 | 1/2 √2 | 1/2 | 0 |
| Cos | 0 | – 1/2 | – 1/2 √2 | – 1/2 √3 | -1 |
| Tan | ∞ | -√3 | -1 | – 1/3 √3 | 0 |
3. Tabel Sin Cos Tan Kuadran 3 dari 180º – 270º
| Sudut | 180º | 210º | 225º | 240º | 270º |
|---|---|---|---|---|---|
| Sin | 0 | – 1/2 | – 1/2 √2 | – 1/2√3 | -1 |
| Cos | -1 | – 1/2√3 | – 1/2√2 | – 1/2 | 0 |
| Tan | 0 | 1/3√3 | 1 | √3 | ∞ |
4. Tabel Sin Cos Tan Kuadran 4 dari 270º – 360º
| Sudut | 270º | 300º | 315º | 330º | 360º |
|---|---|---|---|---|---|
| Sin | -1 | -½√3 | -½√2 | -½ | 0 |
| Cos | 0 | ½ | ½√2 | ½√3 | 1 |
| Tan | ∞ | -√3 | -1 | -1/3√3 | 0 |
5. Tabel Sin Cos Tan Sudut Istimewa
Berikut adalah hasil gabungan tabel yang sudah dijelaskan di atas dari dari tabel sin cos tan sudut istimewa, antara lain:
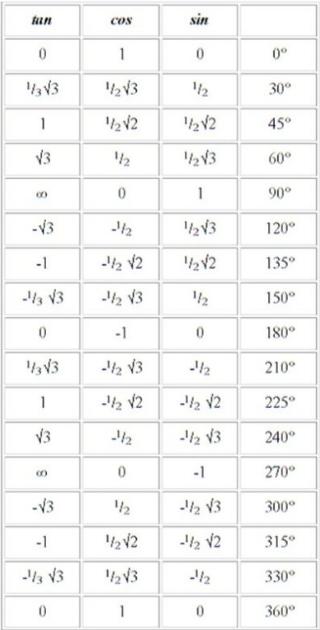
6. Tabel Trigonometri Semua Sudut
Berikut tabel lengkap dan detail mengenai nilai sin cos tan untuk semua sudut mulai dari 0° – 360° untuk memudahkan kalian menemukan nilai sin cos tan dengan tepat dan efektif, antara lain:
a. Sudut 0° sampai 90°
| Sudut | Radian | Sin | Cos | Tan |
|---|---|---|---|---|
| 0° | 0 | 0 | 1 | 0 |
| 1° | 0.01746 | 0.01746 | 0.99985 | 0.01746 |
| 2° | 0.03492 | 0.03491 | 0.99939 | 0.03494 |
| 3° | 0.05238 | 0.05236 | 0.99863 | 0.05243 |
| 4° | 0.06984 | 0.06979 | 0.99756 | 0.06996 |
| 5° | 0.0873 | 0.08719 | 0.99619 | 0.08752 |
| 6° | 0.10476 | 0.10457 | 0.99452 | 0.10515 |
| 7° | 0.12222 | 0.12192 | 0.99254 | 0.12283 |
| 8° | 0.13968 | 0.13923 | 0.99026 | 0.1406 |
| 9° | 0.15714 | 0.1565 | 0.98768 | 0.15845 |
| 10° | 0.1746 | 0.17372 | 0.9848 | 0.1764 |
| 11° | 0.19206 | 0.19089 | 0.98161 | 0.19446 |
| 12° | 0.20952 | 0.20799 | 0.97813 | 0.21265 |
| 13° | 0.22698 | 0.22504 | 0.97435 | 0.23096 |
| 14° | 0.24444 | 0.24202 | 0.97027 | 0.24943 |
| 15° | 0.26191 | 0.25892 | 0.9659 | 0.26806 |
| 16° | 0.27937 | 0.27575 | 0.96123 | 0.28687 |
| 17° | 0.29683 | 0.29249 | 0.95627 | 0.30586 |
| 18° | 0.31429 | 0.30914 | 0.95102 | 0.32506 |
| 19° | 0.33175 | 0.32569 | 0.94548 | 0.34448 |
| 20° | 0.34921 | 0.34215 | 0.93965 | 0.36413 |
| 21° | 0.36667 | 0.35851 | 0.93353 | 0.38403 |
| 22° | 0.38413 | 0.37475 | 0.92713 | 0.40421 |
| 23° | 0.40159 | 0.39088 | 0.92044 | 0.42467 |
| 24° | 0.41905 | 0.40689 | 0.91348 | 0.44543 |
| 25° | 0.43651 | 0.42278 | 0.90623 | 0.46652 |
| 26° | 0.45397 | 0.43854 | 0.89871 | 0.48796 |
| 27° | 0.47143 | 0.45416 | 0.89092 | 0.50976 |
| 28° | 0.48889 | 0.46965 | 0.88286 | 0.53196 |
| 29° | 0.50635 | 0.48499 | 0.87452 | 0.55458 |
| 30° | 0.52381 | 0.50018 | 0.86592 | 0.57763 |
| 31° | 0.54127 | 0.51523 | 0.85706 | 0.60116 |
| 32° | 0.55873 | 0.53011 | 0.84793 | 0.62518 |
| 33° | 0.57619 | 0.54483 | 0.83854 | 0.64974 |
| 34° | 0.59365 | 0.55939 | 0.8289 | 0.67486 |
| 35° | 0.61111 | 0.57378 | 0.81901 | 0.70057 |
| 36° | 0.62857 | 0.58799 | 0.80887 | 0.72693 |
| 37° | 0.64603 | 0.60202 | 0.79848 | 0.75396 |
| 38° | 0.66349 | 0.61587 | 0.78785 | 0.78172 |
| 39° | 0.68095 | 0.62953 | 0.77697 | 0.81024 |
| 40° | 0.69841 | 0.643 | 0.76586 | 0.83958 |
| 41° | 0.71587 | 0.65628 | 0.75452 | 0.86979 |
| 42° | 0.73333 | 0.66935 | 0.74295 | 0.90094 |
| 43° | 0.75079 | 0.68222 | 0.73115 | 0.93308 |
| 44° | 0.76825 | 0.69488 | 0.71913 | 0.96629 |
| 45° | 0.78571 | 0.70733 | 0.70688 | 1.00063 |
| 46° | 0.80318 | 0.71956 | 0.69443 | 1.0362 |
| 47° | 0.82064 | 0.73158 | 0.68176 | 1.07308 |
| 48° | 0.8381 | 0.74337 | 0.66888 | 1.11137 |
| 49° | 0.85556 | 0.75494 | 0.6558 | 1.15117 |
| 50° | 0.87302 | 0.76627 | 0.64252 | 1.1926 |
| 51° | 0.89048 | 0.77737 | 0.62904 | 1.2358 |
| 52° | 0.90794 | 0.78824 | 0.61537 | 1.28091 |
| 53° | 0.9254 | 0.79886 | 0.60152 | 1.32807 |
| 54° | 0.94286 | 0.80924 | 0.58748 | 1.37748 |
| 55° | 0.96032 | 0.81937 | 0.57326 | 1.42932 |
| 56° | 0.97778 | 0.82926 | 0.55887 | 1.48382 |
| 57° | 0.99524 | 0.83889 | 0.5443 | 1.54122 |
| 58° | 1.0127 | 0.84826 | 0.52957 | 1.60179 |
| 59° | 1.03016 | 0.85738 | 0.51468 | 1.66584 |
| 60° | 1.04762 | 0.86624 | 0.49964 | 1.73374 |
| 61° | 1.06508 | 0.87483 | 0.48444 | 1.80587 |
| 62° | 1.08254 | 0.88315 | 0.46909 | 1.8827 |
| 63° | 1.1 | 0.89121 | 0.4536 | 1.96476 |
| 64° | 1.11746 | 0.89899 | 0.43797 | 2.05265 |
| 65° | 1.13492 | 0.9065 | 0.4222 | 2.14707 |
| 66° | 1.15238 | 0.91373 | 0.40631 | 2.24884 |
| 67° | 1.16984 | 0.92069 | 0.3903 | 2.35894 |
| 68° | 1.1873 | 0.92736 | 0.37416 | 2.4785 |
| 69° | 1.20476 | 0.93375 | 0.35792 | 2.60887 |
| 70° | 1.22222 | 0.93986 | 0.34156 | 2.75169 |
| 71° | 1.23968 | 0.94568 | 0.3251 | 2.90892 |
| 72° | 1.25714 | 0.95121 | 0.30854 | 3.08299 |
| 73° | 1.2746 | 0.95646 | 0.29188 | 3.27686 |
| 74° | 1.29206 | 0.96141 | 0.27514 | 3.49427 |
| 75° | 1.30952 | 0.96606 | 0.25831 | 3.73993 |
| 76° | 1.32698 | 0.97043 | 0.2414 | 4.01992 |
| 77° | 1.34444 | 0.97449 | 0.22442 | 4.34219 |
| 78° | 1.36191 | 0.97826 | 0.20738 | 4.71734 |
| 79° | 1.37937 | 0.98173 | 0.19026 | 5.15984 |
| 80° | 1.39683 | 0.98491 | 0.1731 | 5.68998 |
| 81° | 1.41429 | 0.98778 | 0.15587 | 6.33709 |
| 82° | 1.43175 | 0.99035 | 0.1386 | 7.14523 |
| 83° | 1.44921 | 0.99262 | 0.12129 | 8.18379 |
| 84° | 1.46667 | 0.99458 | 0.10394 | 9.56868 |
| 85° | 1.48413 | 0.99625 | 0.08656 | 11.5092 |
| 86° | 1.50159 | 0.99761 | 0.06915 | 14.4259 |
| 87° | 1.51905 | 0.99866 | 0.05173 | 19.3069 |
| 88° | 1.53651 | 0.99941 | 0.03428 | 29.153 |
| 89° | 1.55397 | 0.99986 | 0.01683 | 59.4189 |
| 90° | 1.57143 | 1 | 0 | ∞ |
b. Sudut 90° – 180°
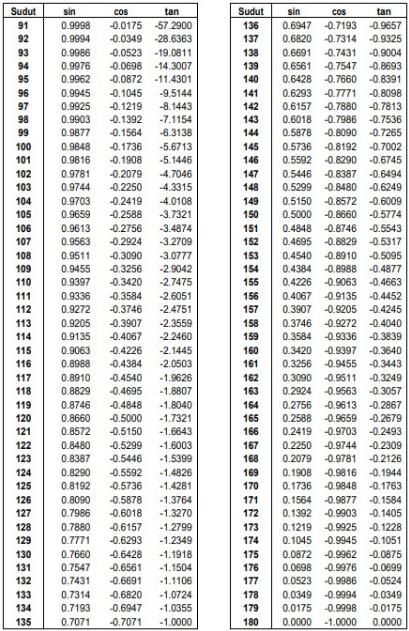
c. Sudut 180° – 270°
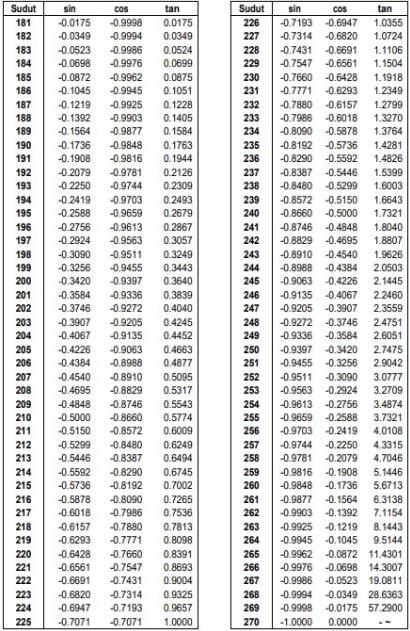
d. Sudut 270° – 360°

7. Tabel Dalam Bentuk Lingkaran
Apabila tabel cos sin tan di atas terlalu panjang untuk kalian hafalkan serta apabila jika metode konsep sudut istimewa tersebut terasa masih sulit, maka kalian dapat menggunakan tabel trigonometri dalam bentuk lingkaran untuk secara langsung dengan melihat nilai sin cos tan dari sudut 360 derajat seperti berikut ini:

Menghitung Sin Cos Tan di Excel
Fungsi sinus, cosinus, dan tangen adalah fungsi dasar di dalam trigonometri.
Excel memberikan fitur fungsi – fungsi trigonometri yang bisa kalian manfaatkan untuk menghitung nilai sinus ,cosinus, dan tangen sebuah sudut.
Operator matematika yang akan sering dipakai di dalam rumus diantaranya seperti:
- + Penjumlahan
- – Pengurangan
- * Perkalian
- / Pembagian
- ^ Perpangkatan
- % Persentase
Proses perhitungan nantinya akan dilakukan sesuai dengan derajat urutan dari operator ini, dimulai dari pangkat (^), kali (*) atau bagi (/), tambah (+) atau kurang (-).
Fungsi Logika (Logical)
Fungsi tersebut dimanfaatkan untuk menentukan sebuah tes secara logika yang dilakukan dalam menampilkan hasil proses.
Pada umumnya hasilnya berwujud karakter yang nilainya True (benar yang bernilai 1) atau False (salah yang bernilai 0).
Fungsi Lookup & Referensi (Lookup & Reference)
Dimanfaatkan untuk menampilkan informasi berdasar di dalam pembacaan dari sebuah table atau kriteria tertentu pada daftar atau tabel.
Fungsi Tanggal & Waktu (Date & Time)
Fungsi yang dipakai di dalam melakukan perhitungan waktu berdasar detik, menit, jam, hari, bulan, serta tahun.
- Sinus
Rumus: =SIN(sudut di dalam radian) atau =SIN(RADIANS (SUDUT))
Contoh:
Carilah nilai sinus dari sudut 0º, 30º, 45º, 60º, dan 90º..!
Jawab:

Di dalam kolom Rumus, nilai A2, A3, dan seterusnya didapatkan dengan cara klik cell di dalam kolom Sudut (º).
- Cosinus
Rumus: =COS (sudut di dalam radian) atau =COS(RADIANS(SUDUT))
Contoh:
Carilah nilai sinus dari sudut 0º, 30º, 45º, 60º, dan 90º..!
Jawab:

di dalam kolom Rumus, nilai A2, A3, dan seterusnya didapatkan dengan cara klik cell di kolom Sudut (º).
- Tangen
Rumus: =TAN(sudut di dalam radian) atau =TAN (RADIANS(SUDUT))
Contoh:
Carilah nilai sinus dari sudut 0º, 30º, 45º, 60º, dan 90º..!
Jawab:

Di dalam kolom rumus, nilai A2, A3, dan seterusnya didapatkan dengan cara klik cell di kolom Sudut (º).
Nilai TAN 90º ialah tak terdefinisi.
- Cosecan
Rumus: =1/SIN (sudut di dalam radian) atau =1/SIN (RADIANS(SUDUT))
Contoh:
Carilah nilai sinus dari sudut 0º, 30º, 45º, dan 90º..!
Jawab:

Di dalam kolom rumus, nilai A2, A3, dan seterusnya didapatkan dengan cara klik cell di kolom Sudut (º).
Nilai COSEC 0º ialah tak terdefinisi.
- Secan
Rumus: =1/COS(sudut di dalam radian) atau =1/COS (RADIANS(SUDUT))
Contoh:
Carilah nilai sinus dari sudut 0º, 30º, 45º, dan 90º..!
Jawab:

Di dalam kolom rumus, nilai A2, A3, dan seterusnya didapatkan dengan cara klik cell di kolom Sudut (º).
Nilai SEC 90º ialah tak terdefinisi.
- Cotangen
Rumus: =1/TAN (sudut di dalam radian) atau =1/TAN (RADIANS(SUDUT))
Contoh:
Carilah nilai sinus dari sudut 0º, 30º, 45º, dan 90º..!
Jawab:

Di dalam kolom rumus, nilai A2, A3, dan seterusnya didapatkan dengan cara klik cell di kolom Sudut (º).
Nilai COT 90º ialah tak terdefinisi.
Mencari Nilai Sin Cos Tan

Untuk memudahkan dalam mengingatnya, biasanya menggunakan istilah SINDEMI, KOSAMI dan TANDESA.
Keterangan:
- sin theta = depan/miring (SINDEMI)
- kos theta = samping/miring (KOSAMI)
- tan theta = depan/samping (TANDESA)
| Sin 0° = 0 Sin 30° = 1/2 Sin 45° = 1/2 √2 Sin 60° = 1/2 √3 Sin 90° = 1 |
Cos 0° = 1 Cos 30° = 1/2 √3 Cos 45° = 1/2 √2 Cos 60° = 1/2 Cos 90° = 0 |
Tan 0° = 0 Tan 30° = 1/3 √3 Tan 45° = 1 Tan 60° = √3 Tan 90° = ∞ |
dan
Cosc A = 1/sin A
Sec A = 1/Cos A
Cotg A = 1/Tg A
Perhatikan skema di bawah.
Langkah – langkah untuk menentukan kuadran sudut atau mengubah sudut ke bentuk yang bersesuaian:
- Kuadran II : 180 – a
- Kuadran III : 180 + a
- Kuadran IV : 360 – a
*) a adalah ibarat angka yang nanti akan digunakan ketika menyelesaikan soal.
Menentukan Tanda (-/+) Nilai Sin Cos Tan
Kalian dapat menggunakan istilah “Semua Sudah Tau Caranya”.
Artinya:
Sesuai dengan urutan kuadran:
- I( semuanya positif)
- II( hanya Sin positif)
- III(hanya Tan positif)
- dan IV (hanya Cos positif)
Catatan: Seluruh langkah – langkah itu dirangkum di dalam skema di atas.
Contoh Soal
Contoh 1
Tentukan nilai Sin 150!
Jawab:
Menentukan kuadran sudut.
Sudut 150 ada di dalam kuadran IIMengubah sudut ke dalam bentuk yang bersesuaian.
Sebab di dalam kuadran II, sudut akan diubah ke dalam bentuk (180 – a), 150 = (180 – 30).Menentukan tanda -/+.
Sin di kuadran II bertanda + Sin 150 = sin (180 –30)= + Sin 30 = 0,5Sehingga Sin 150 = 0,5.
Contoh 2
Tentukan nilai Cos 210!
Jawab:
Menentukan kuadran sudut.
Sudut 210 terletak di dalam kuadran IIIMengubah sudut ke dalam bentuk yang bersesuaian.
Sebab di dalam kuadran, maka sudut diubah ke dalam bentuk (180 + a), 210 = (180 + 30)Menentukan tanda -/+.
Cos di kuadran III bertanda (-)Sehingga Cos 210 = – 1/2 √3
The post Sin Cos Tan appeared first on Yuksinau.
Itulah tadi ulasan tentang Sin Cos Tan yang dapat kami sampaikan untuk Sobat pembaca semuanya. Tak lupa kami ucapkan banyak terima kasih karena sudah mengunjungi situs keminjal. blogspot. com dan membaca urian diatas hingga selesai. Semoga apa yang kami sampaikan diatas dapat menambah wawasan kita semuanya, tertama untuk Anda yang memang sedang mencarinya. Ingat untuk selalu bahagia dan sampai jumpa di postingan selanjutnya.
Post a Comment for "√Sin Cos Tan ~ Keminjal"